homework #1 solutions
The objectives of this homework assignment are the followings:
- Build your own RMarkdown document.
- Master different aspects of RMarkdown syntax.
- Become familiar with GitHub as a collaborative tool.
Note the following requirements:
- All members of the group must commit at least once.
- All commit messages must be reasonably clear and meaningful.
- Your GitHub repository must include at least one issue containing some form of TO DO list.
In your repository, create a RMarkdown file called hw1.Rmd providing an HTML output with the theme cerulean and syntax highlighting tango. This file should contain the following elements:
- A “title” section which should at least include:
- A title (e.g. Homework 1)
- The authors
- The date (think of using
Sys.time())
In order to do so, it is possible to simply write as a header to your RMarkdown:
---
title: "Homework 1"
author: Samuel Orso \& Iegor Rudnytskyi
date: "`r format(Sys.time(), '%d %B, %Y')`"
output: html_document:
theme: cerulean
highlight: tango
---
- A section called “Introduction” where you provide a short summary of the structure of your homework. Moreover, record a short video to introduce your group and include it in your RMarkdown document.
To create a section, use a single hash sign ("#"); to create a subsection, use a double hash sign ("##"). Here, one would write, for the introduction:
# Introduction
Here is the intro. Bla bla bla.
To add a video below, one would add the following nomenclature, for example for a Youtube video:

- A section called “Group Members”. This section should have one sub-section for each group member in your team. For example, a group with three members should have three sub-sections. Each of these sub-sections (named after each group member) should include small biographies containing at least the following elements:
- A picture of your choice (preferably of yourself). Make sure to include a caption for this image.
- A paragraph describing your favorite hobby as well as one interesting fact about yourself (preferably true).
- Your favorite quote in blockquote format. Make sure to reference your quote using BibTex.
- A table having two columns (first column containing the classes you are following this semester; second column containing the time of these classes).
To do the above, one would for example have the following nomenclature, using LaTeX type format for the table:
# Group Members
## Samuel Orso
Lecturer in Data Science at UNIL,...

My hobbies are...
>"Some mathematician, I believe, has said that true pleasure lies not in the discovery of truth, but in the search for it."
>-- Tolstoi
To create a table, one could for example use the kableExtra package and write:
library(knitr)
library(kableExtra)
courses.taken <- c("Applied Mathematics", "Measure Theory", "R for Data Science")
time <- c("08:00", "08:00", "09:00")
df <- data.frame(cbind(courses.taken, time))
colnames(df) <- c("Courses taken", "Time")
kable_styling(kable(df, "html"))
- A section called “RMarkdown Syntax”, where you will demonstrate your RMarkdown skills! In this section make sure to:
- Show an example where the chunk option
cache = Tleads to a misleading answer. This example must be different from the one presented in the textbook.
- Show an example where the chunk option
For example, this can be use to save some time while generating large random vectors. One example where cache=TRUE can be misleading is when you first start by a chunk of the following form, specifying for the option:
set.seed(1)
a <- rexp(100)
and you call a in another chunk, say the following one, with option cache=TRUE:
(b <- log(a))
without adding as option dependson=(name of the first chunk), since if you first knit with 100 randomly generated exponential numbers and you then change a to rexp(1000), it will cache the value of a and only show you b accordingly.
- Simulate 300 random samples from a distribution that is uniform on [-1, 1] interval using the function
runif(). Store these 300 values in a vector calledx. Then, compute the empirical median, mean and variance ofx. Are these results different from 0, 0 and 1/3 (their respective theoretical values)? Is this result surprising? Justify your answer.
Here is the code to do so:
set.seed(1)
x <- runif(n = 300, min = -1, max = 1)
empmean <- mean(x)
empmed <- median(x)
empvar <- var(x)
The values are somewhat different from 0, 0 and 1/3 respectively, not so much but this variation is due to the fact that we only compute sample estimates of population values for the values above. Therefore, there is a natural variation.
- Include a graph showing the density estimation of
x(make sure to include a caption to this figure). You can use the R functiond <- denstiy()with default parameters, and theplot(d)function. Why does the estimated density exceed the [-1, 1] interval?
One would use the following command:
d <- density(x)
plot(d, main = "Density")
adding as an option to this chunk the option fig.cap="Density estimation of x" to display a caption to this figure.
By default density estimator uses “gaussian” kernel to construct the curve. Therefore, the points that are close to the borders (-1 and 1) add extra noise, which expands outside of the original interval. This noise may be reduced by decreasing the bandwidth bw, as well as choosing a kernel with finite support, i.e. rectangular or epanechnikov.
- Include the following equation
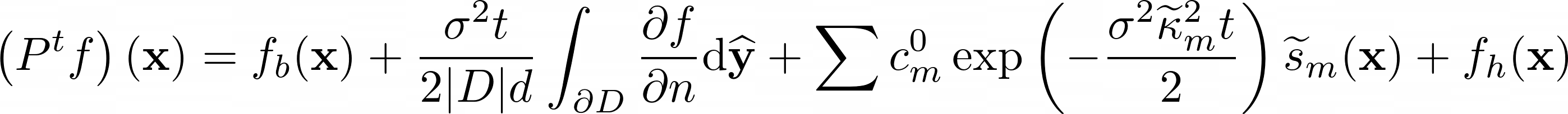 :
:
\[
\begin{aligned}
\left( P^t f \right) ( \mathbf{x} ) =
f_b ( \mathbf{x} ) +
\frac{\sigma^2 t}{2 |D| d} \int_{\partial D}
\frac{\partial f}{\partial n} \mathrm{d} \widehat{\mathbf{y}} +
\sum c_m^0 \exp \left(
- \frac{\sigma^2 \widetilde{\kappa}_m^2 t}{2}
\right)
\widetilde{s}_m ( \mathbf{x} )
+ f_h ( \mathbf{x} )
\end{aligned}
\]
- Include the following in-line equation:
To do so, use the LaTeX nomenclature as follow:
$\hat{f}(\xi) = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^\infty f(x) \, e^{-i x \xi} \, \mathrm{d} x.$
- Include the following text in blue: “The degree of civilization in a society can be judged by entering its prisons.”, Fyodor Dostoevsky
Write:
<span style="color:green">"The degree of civilization in a society can be judged by entering its prisons.", Fyodor Dostoevsky text</span>
- Include a “More info” button with hide/unhide functionality.
To do so, use:
<button data-toggle="collapse" data-target="#demo">More info</button>
<div id="demo" class="collapse">
Some additional info...
</div>
- Include a “color box”" with some text.
To do so, use:
<div class="alert alert-danger">
<strong>Some important Info:</strong> something
</div>